Als beton wordt belast, vervormt het. Hoeveel het vervormt, is mede afhankelijk van de stijfheid van het materiaal. Deze eigenschap drukken we uit in de elasticiteitsmodulus (E-modulus). Een constructeur gebruikt de E-modulus om de vervorming, doorbuiging en stabiliteit van een constructie te berekenen en te beheersen. In sommige situaties, zoals voor de overlaging van stalen brugdekken, worden hoge eisen gesteld aan de stijfheid van het beton. In deze Betoniek laten we zien dat deze eigenschap met het ontwerp van het betonmengsel aardig te sturen is. We beschrijven achtereenvolgens de eigenschap, de wet van Hooke, de factoren die van invloed zijn op de E-modulus van beton, hoe je eraan rekent volgens de Eurocode, en twee praktijkvoorbeelden waarin de betontechnoloog een specifieke E-modulus heeft gerealiseerd.
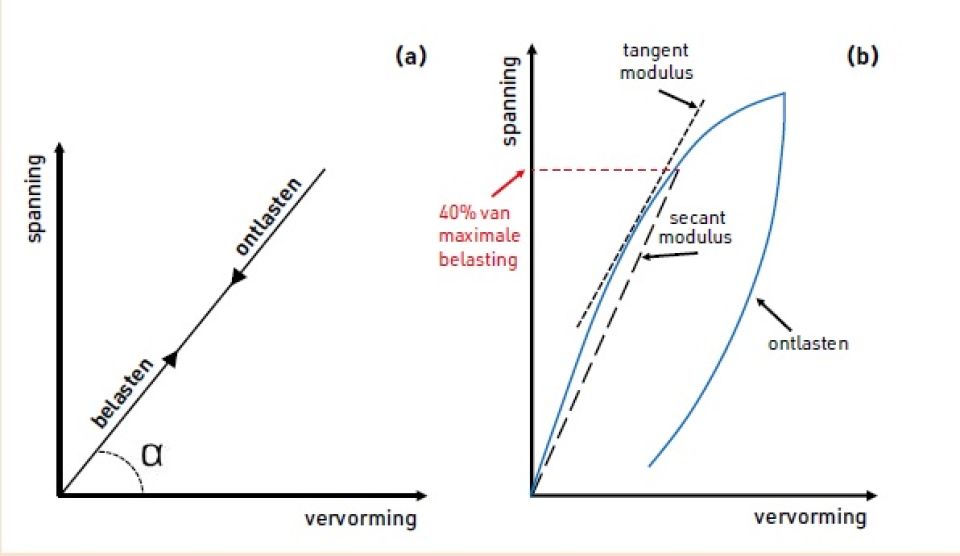
1. Schematische weergave spanning-vervormingsrelatie van (a) een lineair elastisch materiaal, zoals staal, en (b) van het niet-lineair elastische samengestelde materiaal beton
De E-modulus is een maat voor de stijfheid van een materiaal en bepaalt hoeveel het vervormt onder een bepaalde belasting. Dat kan een externe druk- of trekbelasting zijn of eigen gewicht. De E-modulus is het quotiënt van de spanning σ en de vervorming ε (formule 1). In de constructieve berekening is het belangrijk de E-modulus te kennen, omdat de stijfheid van het materiaal mede bepalend is voor de doorbuiging van een element. Te grote doorbuiging kan leiden tot ongewenste vervormingen, schade aan afwerkingen en zelfs constructief falen, maar ook tot een gevoel van onveiligheid en ongemak.
Het vervormingsgedrag van materialen verschilt. Zo vertonen homogene materialen zoals staal een zuiver elastische vervorming (fig. 1a). Zuiver elastisch betekent dat het materiaal na het wegnemen van een bepaalde belasting weer terugkeert in zijn originele vorm. Dit lineaire vervormingsgedrag geldt binnen het elastisch gebied van het materiaal. Elk materiaal, ook staal, kun je nog verder vervormen, tot buiten het elastisch gebied. Dan is er sprake van blijvende rek en keert het materiaal niet meer terug in zijn oorspronkelijke vorm.
Beton is een heterogeen samengesteld materiaal. Het is niet zuiver elastisch en vertoont geen lineair vervormingsgedrag. Beton keert dus na het wegnemen van een bepaalde belasting niet volledig terug in zijn originele vorm. De spanning-vervormingsrelatie voor beton is vereenvoudigd en schematisch weergegeven in figuur 1b, waarbij beton tot voorbij het elastisch gebied is belast en de belasting vervolgens weer is weggehaald.
De blijvende vervorming van beton is tot een belasting van 40% van zijn maximale belastbaarheid zeer gering (dit komt later ook terug in fig. 8). Binnen dit bereik is de spanning-vervormingsrelatie bij benadering lineair te noemen en wordt ter vereenvoudiging aangenomen dat het beton zich gedraagt als een lineair elastisch materiaal (fig. 1a). De E-modulus in dit gebied noemen we de secant-modulus en kan worden gekarakteriseerd volgens de wet van Hooke (zie hierna).
In figuur 1b is af te lezen dat de lijn voorbij 40% van de maximale belastbaarheid vlakker gaat lopen en dat de E-modulus in functie van de vervorming afneemt. In dit gebied moet de exacte waarde voor de E-modulus worden bepaald op basis van een puntmeting en de raaklijn op dat punt. De E-modulus in dit gebied noemen we de tangent-modulus. In het vervolg van deze Betoniek wordt met E-modulus de secant-modulus bedoeld, tenzij specifiek anders benoemd.
Reacties
Janneke - Betoniek 05 september 2024 10:33
Beste Jos en Gerrit Jan, De pdf is inmiddels toegevoegd, dus deze kun je nu wel downloaden. Excuus voor de vertraging. Groet, Janneke
Gerrit Jan Holtland - Mobilis B.V. 04 september 2024 09:05
Blijkbaar niet meer als pdf. Je kunt het altijd kopiëren en plakken in een Word-document.
Jos van Schijndel - SKG-IKOB Certificatie 03 september 2024 16:16
ik wil deze Betoniek graag dowloaden, kan dat niet meer?